数学検定・算数検定とは
算数の実力を知ることができる、全国レベルの検定です。
算数検定は、正式名称を「実用数学技能検定」といいます。
実用数学技能検定には、1級から11級と準1級、準2級、かず・かたち検定のゴールドスター、シルバースターを合わせて全部で15の階級があり、そのうちの算数領域である6級から11級、かず・かたち検定を、通称「算数検定」と呼んでいます。
数学・算数の実用的な技能(計算・作図・表現・測定・整理・統計・証明)を測る記述式の検定として、年間30万人以上の方が受検しています。
水田塾は数学検定の認定会場です
算数・数学の学習をとおして身に付く力
算数・数学の学習をとおして、計算の力や図形の問題を解く力が身につくのはもちろんのこと、以下のようなさまざまな能力が身につきます。
-
その1
道筋を立てて考えられる「論理的思考力」
-
その2
自分の考えを表現できる「コミュニケーション能力」
-
その3
文章問題で、本当に問われていることを導き出せる「読解力」
-
その4
一度使用した解き方を他の問題でも使用できる「応用力」
-
その5
一方向からの視点だけでは解けない問題に取り組める「多角的な視点」
これらの5つの能力はのちの将来に必ず役立つものですが、これらの能力の必要性を子どものうちに理解することは難しいことです。
なので「数の楽しさ」「数字の不思議」により幼いころからたくさん触れておくことで、苦手意識を持たずに算数好き・数学好きに成長し、これらの大切な能力を自然と身につけていけるのではないかと考えます。
目安となる学年と階級
小学1年生が多くチャレンジしているのは・・・11級
小学2年生が多くチャレンジしているのは・・・10級
小学3年生が多くチャレンジしているのは・・・9級
小学4年生が多くチャレンジしているのは・・・8級
小学5年生が多くチャレンジしているのは・・・7級
小学6年生が多くチャレンジしているのは・・・6級
数学検定のメリット
数学検定には、いくつかのメリットがあります。
-
その1
入試優遇や単位認定が受けられる!
入試優遇制度では、特定の階級に合格すると、大学・短期大学・高等学校・中学校などの一般・推薦入試において優遇措置や評価などを受けることができます。
全国の高等専門学校・高等学校・中学校720校以上の、大学・短期大学・専門学校440校以上の学校で、この制度が導入されています。単位認定制度では、大学・高等学校・高等専門学校などで、一定の階級の実用数学技能検定取得者に対して、特定の科目の単位取得が認められます。
全国の大学・高等専門学校・高等学校310校以上の学校で、この制度が導入されています。 -
その2
高等学校卒業程度認定試験で「数学」の試験免除が受けられる!
実用数学技能検定1級、準1級、または2級取得で、文部科学省が行う「高等学校卒業程度認定試験(旧「大検」)」の必須科目「数学」が試験免除となります。
これは平成17年1月31日付で文部科学省が告示したものです 。
文部科学省では生涯学習社会を築いていくためには、さまざまな学習の成果が適切に評価されるとともに、この成果を広く社会で活用することが重要だとしており、その中で実用数学技能検定も引き続き活用されることとなりました。
高等学校卒業認定試験で実用数学技能検定の合格を証明する場合には、「合格証明書」が必要となります。
目安となる学年と階級
中学1年生が多くチャレンジしているのは・・・5級
中学2年生が多くチャレンジしているのは・・・4級
中学3年生が多くチャレンジしているのは・・・3級
高校1年生が多くチャレンジしているのは・・・準2級
高校2年生が多くチャレンジしているのは・・・2級
高校3年生が多くチャレンジしているのは・・・準1級
大学・社会人の方
-
その1
数学検定は就職に有利!
企業の採用資料として多く活用されている「SPI試験の非言語分野」に3級の出題範囲が53%、準2級では74%が共通しています。
「数学検定」を受検することで、SPI試験の対策にもつながるといえます。 -
その2
数学力はIT系などの職業にも役立ちます!
プログラマーやインフラエンジニア、システムエンジニアなどの専門職業には、特定のベンダーやトレンドにとらわれない、「普遍的なスキル=数学力」が必要です。数学知識の本質を理解しているかどうかで、エンジニアの質に大きな差が生まれてしまいます。
現在エンジニアなどの職業に就いている方も、将来就くことを望んでいる方も、「数学検定」で技術者としての能力の“底上げ”をし、自身の数学力を高めることができます。
目安となる条件と階級
理数系の大学に通っている方は・・・1級
数学Ⅲの見直しをしたい方は・・・・準1級
SPI試験の対策に活用したい方は・・3級・準2級
IT技術者として、数学力を高めたい方
高校3年(数学Ⅲ)程度の・・・準1級
高校2年(数学Ⅱ・数学B)程度の・・・2級
高校1年(数学Ⅰ・数学A)程度の・・・準2級
検査結果の通知
受検後も引き続き算数・数学の学習に励んでいただけるよう、検定結果の通知として、以下のものを送付しております。
※合格証・合格証明書は該当者に限ります。


合格証明書
家族合格表彰について
受検後も引き続き算数・数学の学習に励んでいただけるよう、検定結果の通知として、以下のものを送付しております。
※合格証・合格証明書は該当者に限ります。

家族合格表彰
この「家族合格表彰」は、団体受検・個人受検を問わず、同じ年度内(4月から翌年3月)に実用数学技能検定(数学検定・算数検定)に合格したご家族を表彰する制度です。
ご家族で申請いただくと、合格されたご家族全員のお名前を印字した「家族合格表彰」の賞状を発行いたします(無料)。同年度内の合格であれば、検定日が違っていても構いません。
ご家族の皆で合格した記念に、ぜひご利用ください。
受検資格について
原則として受検資格を問いません。どなたでもどの級からでも受検いただけます。
※ただし、時代の要請や学習環境の変化などにより、公益財団法人日本数学検定協会が必要と認めるときはこの限りではありません。

年間30万人を越える方が受験する、実用数学技能検定。
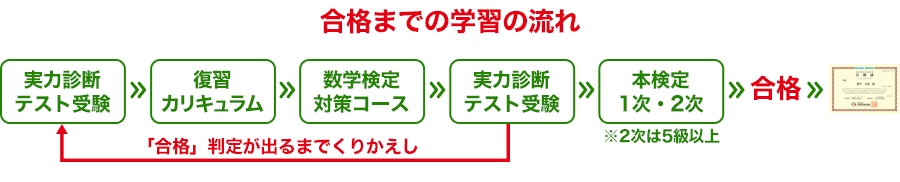
今回、検定を実施している「日本数学検定協会」と「水田塾のオンライン学習システム」がコラボして、受検を検討している皆さんを合格へと導く、「算数検定・数学検定 実力診断テスト」が完成しました!
診断テストに加えて、復習カリキュラム、対策コースの受講と、受検を検討中の皆さんに必要なものがすべて入ったちょっと欲張り・贅沢な内容です。
受検級を決めたら、早速今日から、合格目指して対策を始めましょう!
だから身につく、診断テスト4つのポイント!

日本数学検定協会監修のもとに厳選されたテスト問題。
本検定同様の内容・難易度のテストを受けることができます。

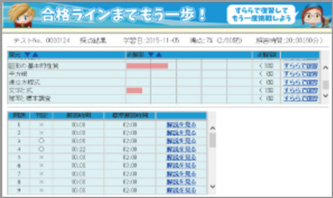
テスト終了後には、本検定に向けて見直すべきポイントや克服するための学習カリキュラムが提示されるので、効率よく本検定までの学習計画を立てることができます。
※「合格ライン」に達すると、「合格」が結果に表示されます。

より万全の準備をしたいときには、過去の出題問題を分析し、必要となる項目を絞り込んだ、「数学検定対策コース」がおすすめ。
単なる演習だけではなく、くわしレクチャーのついて対策コースで、出題が予想される項目をしっかりと理解したうえで実力を養成。
本検定に向けて万全な準備ができます。

診断テストはいつでも何度でも受験することが可能です。
もちろん復習や対策コースも受け放題!
診断テストと復習・対策コースを繰り返し活用すれば、合格がどんどん近づいてきます!




| 実用数学技能 検定の階級 |
算数検定 | |||||
|---|---|---|---|---|---|---|
| 6級 | 7級 | 8級 | 9級 | 10級 | 11級 | |
| 目安となる学年 | 小学校 6年程度 |
小学校 5年程度 |
小学校 4年程度 |
小学校 3年程度 |
小学校 2年程度 |
小学校 1年程度 |
| 出題数 | 30問 | 20問 | ||||
| 合格基準 | 全問題の70%程度 | |||||
| 実用数学技能 検定の階級 |
算数検定 | ||
|---|---|---|---|
| 6級 | 7級 | 8級 | |
| 目安となる学年 | 小学校 6年程度 |
小学校 5年程度 |
小学校 4年程度 |
| 出題数 | 30問 | ||
| 合格基準 | 全問題の70%程度 | ||
| 実用数学技能 検定の階級 |
算数検定 | ||
|---|---|---|---|
| 9級 | 10級 | 11級 | |
| 目安となる学年 | 小学校 3年程度 |
小学校 2年程度 |
小学校 1年程度 |
| 出題数 | 20問 | ||
| 合格基準 | 全問題の70%程度 | ||
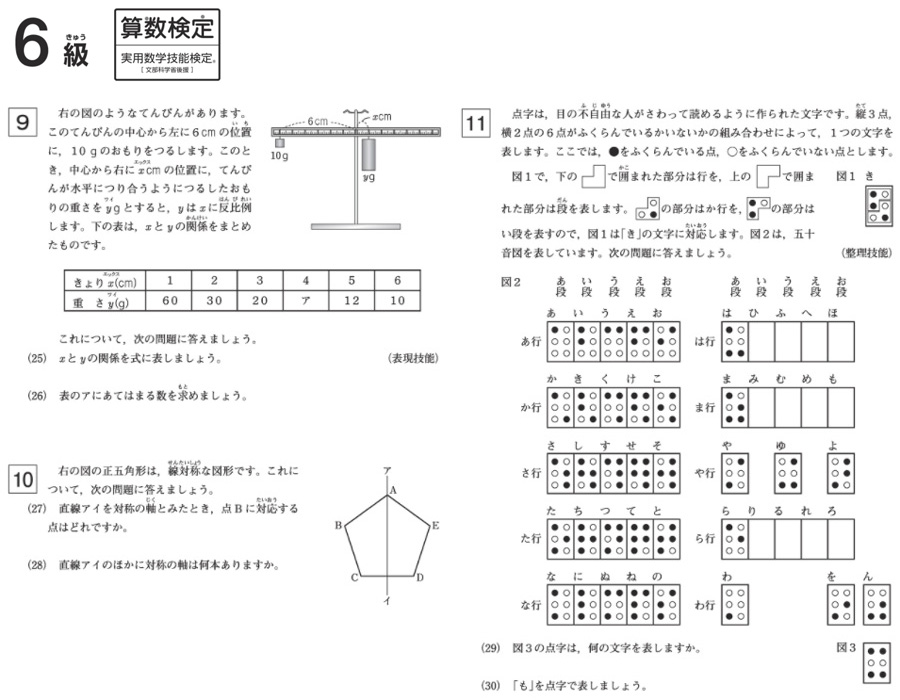
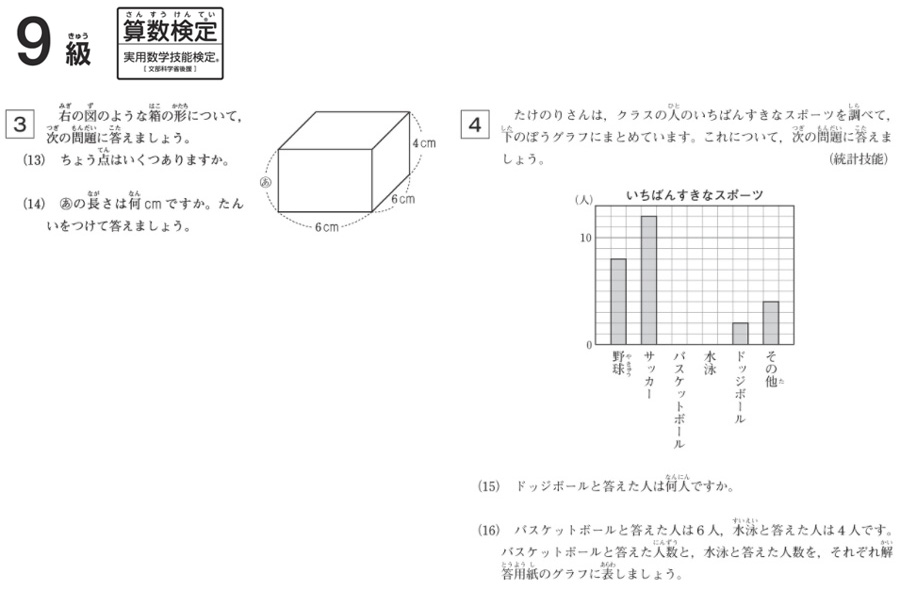
算数検定の過去の問題


数学を学習するときのポイントは?
ポイント1 自分の頭でしっかりと考えること
数学を学ぶときに大事なのは、公式をただ覚えて終わりにしないことです。どうしてそうなるのかを考え、公式をしっかりと理解することが大切です。覚えることは、理解することではありません。たくさん考えて理解して初めて、自分の知識となり、それを応用することができるのです。

ポイント2 自分の考えをきちんとまとめて、伝えられるようになること
計算問題をただ解くだけが、数学ではありません。これから学ぶ数学の中には、文章で説明したり、問題文から計算式をつくったりする問題がたくさんでてきます。そんな問題を解くポイントになるのが「考えを伝えること」。ぼんやりとしたあいまいな説明では、相手にうまく伝わりません。なぜそうなったのか、なぜそう考えたのかをきちんと整理し、結果どういう答えが導かれたのかを筋道を立てて説明できるようになりましょう。

ポイント3 あきらめずに向き合うこと
わからない問題が出てきたときに、最初からあきらめないことも、学習するときの大切なポイントです。まずは問題にしっかりと向きあい、自分なりに理解しようとしてみましょう。わからないときも、何がわからないのかをしっかりと説明できるようにすることで、先生に明確な質問ができます。


| 実用数学技能 検定の階級 |
数学検定 | ||||||
|---|---|---|---|---|---|---|---|
| 1級 | 準1級 | 2級 | 準2級 | 3級 | 4級 | 5級 | |
| 目安となる学年 | 大学程度 一般 |
高校3年程度 (数学Ⅲ程度) |
高校2年程度 (数学Ⅱ・数学B程度) |
高校1年程度 (数学Ⅰ・数学A程度) |
中学校 3年程度 |
中学校 2年程度 |
中学校 1年程度 |
| 出題数 | 1次:7問 2次:2題必須・5題から2題選択 |
1次:15問 2次:2題必須・5題から3題選択 |
1次:15問 2次:10問 |
1次:30問 2次:20問 |
|||
| 合格基準 | 1次:全問題の70%程度 2次:全問題の60%程度 |
||||||
| 実用数学技能 検定の階級 |
数学検定 | |||
|---|---|---|---|---|
| 1級 | 準1級 | 2級 | 準2級 | |
| 目安となる学年 | 大学程度 一般 |
高校3年程度 (数学Ⅲ程度) |
高校2年程度 (数学Ⅱ・数学B程度) |
高校1年程度 (数学Ⅰ・数学A程度) |
| 出題数 | 1次:7問 2次:2題必須・5題から2題選択 |
1次:15問 2次:2題必須・5題から3題選択 |
1次:15問 2次:10問 |
|
| 合格基準 | 1次:全問題の70%程度 2次:全問題の60%程度 |
|||
| 実用数学技能 検定の階級 |
数学検定 | ||
|---|---|---|---|
| 3級 | 4級 | 5級 | |
| 目安となる学年 | 中学校 3年程度 |
中学校 2年程度 |
中学校 1年程度 |
| 出題数 | 1次:30問 2次:20問 |
||
| 合格基準 | 1次:全問題の70%程度 2次:全問題の60%程度 |
||
数学検定の過去の問題

漢字検定について

将来に役立つ5つの力が身につく。
問題に取り組み解いていくなかで「倫理的思考」「コミュニケーション能力」「読解力」「応用力」「多角的な視点」が身につきます。
入試優遇や単位認定・試験免除などが可能に。
全国の高校や大学では、特定の級に合格すると、入試における優遇制度や単位認定制度を設けているところが多数あります。
また、1級・準1級・2級のいずれかの取得で、高等学校卒業程度認定試験(旧「大検」)の「数学」が試験免除となります。
就職や就職後の業務でも役立ちます。
就職試験でよく使われるSPI。そのなかの非言語分野の出題範囲と、3級は53%・準2級は74%が共通しており、SPI試験の対策としても数学検定はとても有効です。
また、エンジニア・プログラマーといったIT系の職種はもちろん、それ以外の職種においても、数学の力は多くのシーンで求められ、その力を身につけるにも数学検定は最適です。